Exercício 1
Resolva, EM 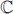 , Como Equações:
1.
, Como Equações:
1.  2.
2.  3.
3. 
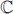 , Como Equações:
, Como Equações:


Exercício 2
Equacionaríamos OS Números Complexos  e
e  .
1. Represente na forma Algébrica
.
1. Represente na forma Algébrica  ,
,  e
e  .
2. Sendo determinar e de MoDo Que SEJA UM imaginário puro.
.
2. Sendo determinar e de MoDo Que SEJA UM imaginário puro. 



 e
e  .
. ,
,  e
e  .
.



Exercício 3
Represente geometricamente (diagrama de Argand) o Conjunto dos pontos do plano Definido pelas Imagens dos Complexos  Opaco satisfazem CONDIÇÔES Como:
Opaco satisfazem CONDIÇÔES Como:
 Opaco satisfazem CONDIÇÔES Como:
Opaco satisfazem CONDIÇÔES Como:
1. 

2. 

3. 

Nenhum comentário:
Postar um comentário