Números Complexos

Sendo a e b números reais e i a unidade imaginária , chamamos de números complexo a todo número Z na forma 

Z=a+bi  onde: a é a parte real

                     b é a parte imaginária

Exemplos: 

4+3i, 5-i, 0+7i=7i , -3+0i=-3 é importante observar que os números imaginários reais são números complexos.

Assim, dado o número complexo Z=a+bi, temos:

• Se b=0 --> Z=a (Z é um número real ).

Exemplos:5+0i=5, Z=-3/2+0i=3/2

• Se a≠0 e b ≠0 --> Z=a +bi ( Z é imaginário).

Exemplo: 5+ 2i, -4+7/5i

• Se a=0 e b≠0 ---> Z=bi(Z é imaginário puro).

Exemplo:

5i, -i

O conjunto dos números complexos , que se indica por  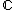(  ), é formada pela reunião dos conjuntos dos números reais.

Observação :Dizemos que Z= a+bi é a forma algébrica de um número complexo.

Igualdade de Dois números

Dois números complexos são iguais se e somente se suas partes reais e imaginárias são respectivamente guais.

Sendo Z1=a+bi e Z2=c+di:

Z1=Z2 se e somente a=c e b = d

Fonte:Coleção Horizontes, Jorge Daniel Silva & Valter dos Santos Fernandes Obra Executada nas oficinas do Instituto Brasileiro de edições Pedagógicas .