Exercício 1
1. SEJA  .
.
 .
. 



2. 




3.



Exercício 2
1.




2.

Para Opaco  SEJA UM imaginário puro um verdadeiro contraditório nula TEM Que Ser EO coeficiente da Parte Imaginária TEM Que Ser Diferente de zero. Logo:
SEJA UM imaginário puro um verdadeiro contraditório nula TEM Que Ser EO coeficiente da Parte Imaginária TEM Que Ser Diferente de zero. Logo:
 SEJA UM imaginário puro um verdadeiro contraditório nula TEM Que Ser EO coeficiente da Parte Imaginária TEM Que Ser Diferente de zero. Logo:
SEJA UM imaginário puro um verdadeiro contraditório nula TEM Que Ser EO coeficiente da Parte Imaginária TEM Que Ser Diferente de zero. Logo:

Exercício 3
1.
SEJA  .
.
 .
.
• 

•


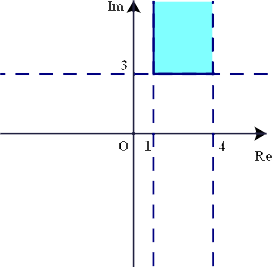
2.
SEJA  .
.
 .
.
•

•

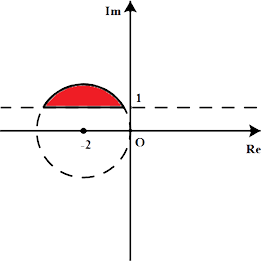
3.

•

•

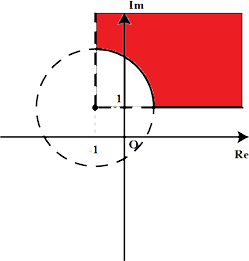
Fonte:http://www.atividadesdematematica.com/banco-questoes-12-ano-complexos/numeros-complexos-exercicio-1
Nenhum comentário:
Postar um comentário