Números Imaginários
No conjunto dos números reais (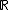 
) a 
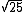é igual a 5, mas qual é a 
?
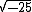Como sabemos, não existe a raiz quadrada real de um radicando negativo com índice par. No conjunto dos números reais o máximo que podemos fazer é simplificar o radical desta forma:
Ainda assim o fator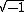 
não é um número real, pois o radicando -1 é um número negativo.
Para maiores informações sobre como retiramos o número 5 do radical, você pode consultar o nosso artigo sobre a radiciação e suas propriedades.
Unidade Imaginária
A solução para este tipo problema surgiu com a criação dos números imaginários, cuja unidade imagináriarepresentada pela letra i, é igual a .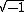
Utilizando-se do conceito de número imaginário podemos dizer que a 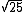é igual a 5i, pois:
Agora vamos solucionar a equação do segundo grau abaixo:
O primeiro passo é calcularmos o seu discriminante:
Como o discriminante é negativo, a equação não possui raízes reais:
Mas possui raízes imaginárias ao substituirmos 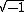por i:
Nos dois exemplos acima, 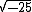e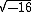 
, temos um radicando que é o valor simétrico de um quadrado perfeito, ou seja, o oposto de 25 e de 16, que são quadrados perfeitos, mas mesmo que não o fossem, ainda assim poderíamos trabalhar com o conceito de números imaginários.
Vejamos o exemplo do número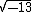 
:
Observe que não eliminamos o radical, pois o número 13 não é um quadrado perfeito, mas agora temos um radicando positivo.
Quadrado perfeito é qualquer número inteiro maior ou igual a zero, que podemos representar pelo quadrado de um número também inteiro, por exemplo, 144 é um quadrado perfeito, pois: 144 = 122
Há casos em que alguns fatores do número saem do radical e outros fatores não. Veja o exemplo do número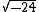 
:
Fonte: http://www.matematicadidatica.com.br/ConjuntoNumerosComplexos.aspx
Nenhum comentário:
Postar um comentário