Módulo de um número complexo
Chama-se módulo ou valor absoluto de um número complexo Z= a+bi ao número |z|=
.
.
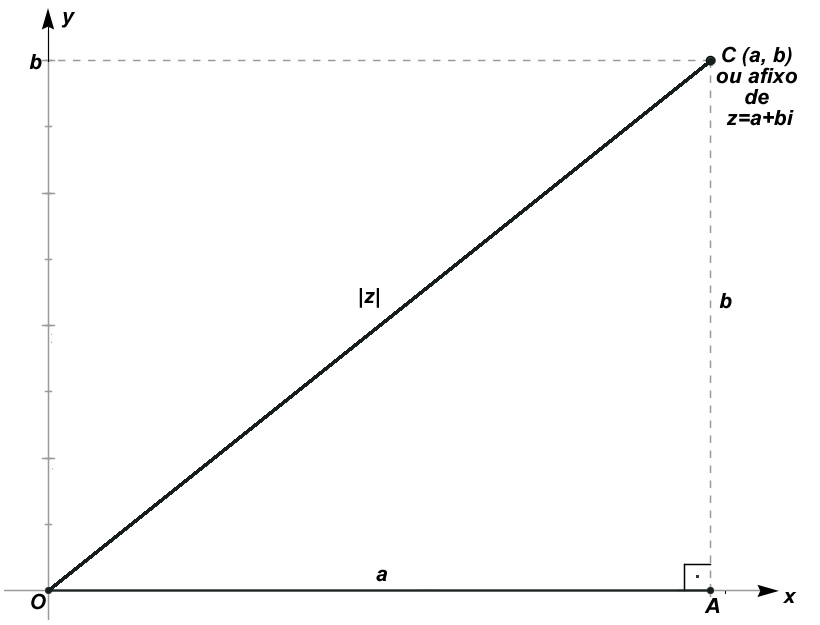Observe: |z| é a distância doa fixo do número complexo á origem do sistema cartesiano z²=a²+b²
Exemplos:
Determine o módulo dos seguintes números complexos:
a)Z=3+4i
|z|=√ 3²+4²=
|z|=√ 9+16=
|z|=√ 25
|z|=5
Agurmento de um número Complexo
Chamamos de argumento de um número complexo Z= a+bi, não nulo, ao angulo o , onde o 
o 2
, tal que:
2, tal que: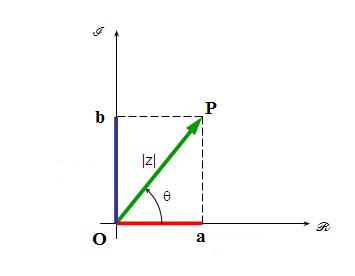
cos ø=a
z
e sen ø=b
z
Exemplo:
Determine o argumento dos seguintes números complexos:
a) Z=1+i
a=1
b=1
z=√1²+1²= z=√2
z=√1²+1²= z=√2
cos o=a
z
cos o=1
√2
cos o=√2
2
sen o=b
z
sen o= 1
√2
sen o=√2
2
Sendo , o =
Forma Trigonométrica
Seja o complexo Z=a+bi.
Sabemos que:
cos o a a=z cos o
z
sen o b b=z sen o
z
Substituindo esses valores de a e b em Z=a+bi, temos:
Z= z. cos o + i.z.sen o , colocando z em evidência, temos:
Z=z(cos o + i sen o) expressão esta, chamada de forma trigonométrica ou polar do número complexo Z= a+ bi.
Exemplo:
Passar para a forma trigonométrica o complexo Z=2+2i.
Cálcuo de z
z=√a²+b² z= √2²+2² z=√8 z=2√2
Cálculo de o
cos o = a cos o = 2 = 1 cos o = √2
z 2√2 √2 2
sen o =a sen o 2 = 1 sen o =√2
z 2√2 √2 2 o =
Logo , a forma trigonométrica de Z= 2 + 2i é:
Z=2√2(cos
Fonte:http://www.mundoeducacao.com/matematica/o-modulo-numero-complexo.htm
Fonte:Coleção Horizontes, Jorge Daniel Silva & Valter dos Santos Fernandes Obra Executada nas oficinas do Instituto Brasileiro de edições Pedagógicas .
Nenhum comentário:
Postar um comentário